Contents:

Introduction to Applied Statistics

Business Analytics Capability Chart

Applied statistics is the use of statistical techniques to solve real-world problems across various fields such as business, engineering, medicine, and social sciences. This involves collecting, analyzing, and interpreting data to make informed decisions and predictions. By leveraging statistical methods, organizations can optimize operations, improve quality, and gain insights that drive strategic decisions.

[!NOTE]
Reference and Details: Applied Statistics Project

Reference and Details: Online Statistics Education

Key Features of Applied Statistics

1. Data Collection

The foundation of applied statistics is the systematic collection of data. This phase is crucial as the quality of data directly impacts the reliability of statistical analysis.

2. Data Analysis

Data analysis involves summarizing and interpreting the data to extract meaningful insights.

3. Probability

Probability theory underpins many statistical methods, providing a framework for making inferences about populations based on sample data.

4. Regression Analysis

Regression analysis is a powerful tool for examining the relationships between variables.

5. ANOVA (Analysis of Variance)

ANOVA techniques are used to compare means among different groups.

6. Non-Parametric Methods

Non-parametric methods are useful when data doesn’t meet the assumptions of parametric tests.

7. Time Series Analysis

Time series analysis involves studying data points collected or recorded at specific time intervals.

8. Multivariate Analysis

Multivariate analysis techniques handle multiple variables simultaneously to understand complex relationships.

9. Statistical Software and Tools

Various software and tools are available to perform statistical analysis efficiently.

Applied Statistics: Thinking, Not a Toolbox

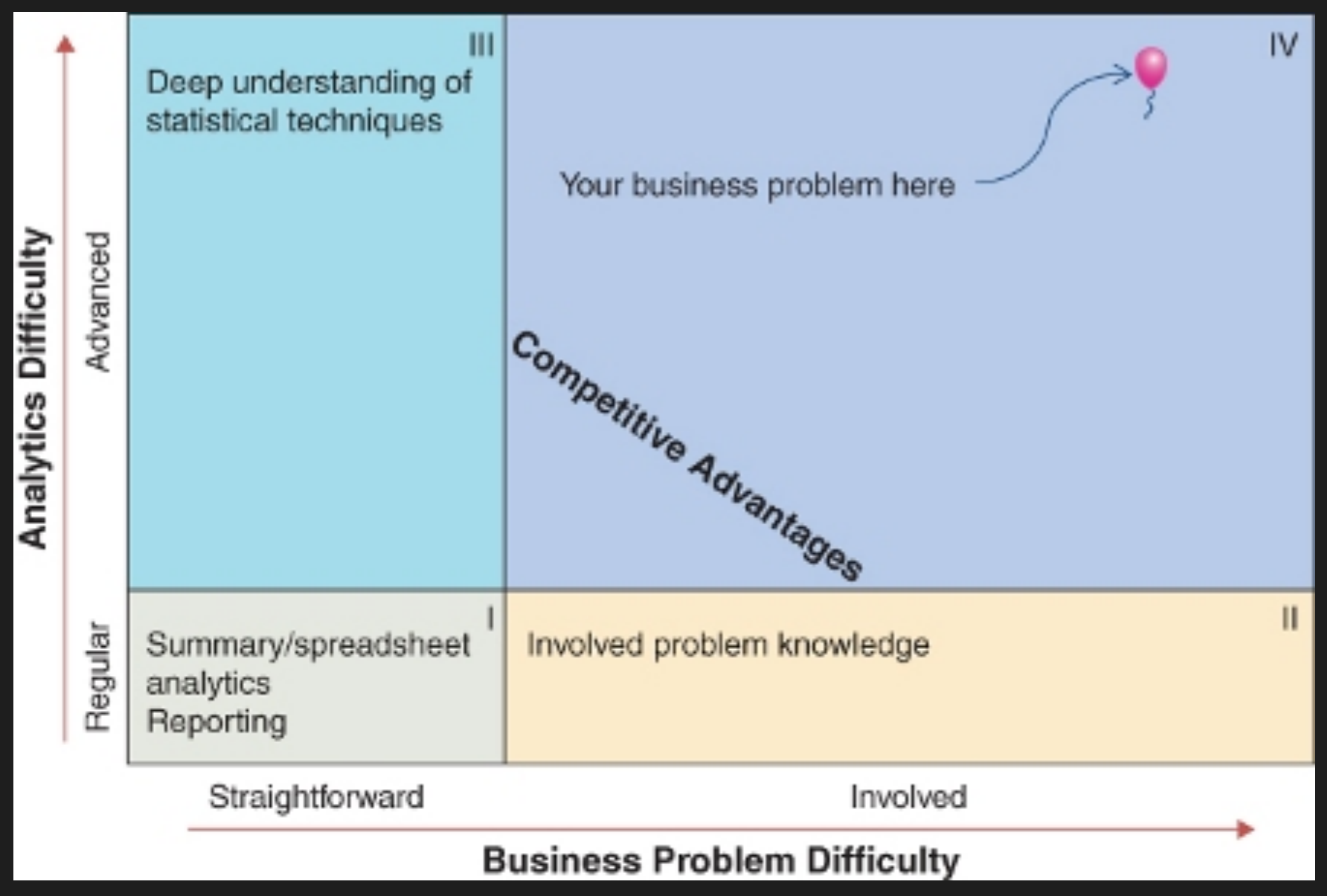
Image Applied statistics is more about thinking critically and approaching problems with a statistical mindset rather than just using a set of tools. The key points include:

  1. Mindset Over Tools: Applied statistics involves a way of thinking and problem-solving that integrates statistical methods with the context of the problem. It’s about understanding the underlying principles and making informed decisions based on statistical reasoning.
  2. Problem Understanding: Effective application of statistics requires a deep understanding of the problem at hand, including the domain context. It’s crucial to define the problem clearly, choose appropriate methods, and interpret results correctly.
  3. Modeling and Assumptions: Building statistical models involves making assumptions about data and processes. The importance of understanding these assumptions and their implications for the validity of the results is emphasized.
  4. Data Exploration: Exploratory data analysis (EDA) is essential for understanding the data before applying statistical techniques. This step helps in identifying patterns, anomalies, and insights that guide the analysis.
  5. Communication: Communicating statistical findings effectively is as important as the analysis itself. Results should be presented in a way that is understandable to stakeholders, highlighting key insights and their implications.
  6. Continuous Learning: Applied statisticians must stay updated with evolving methods and best practices. The field of statistics is dynamic, and ongoing learning is necessary to apply the latest techniques effectively. Statistical Thinking—understanding the principles, context, and implications of analysis—is fundamental to applied statistics, rather than just relying on statistical tools and software.

Here is a mix of common statistics tools and the overlapping genealogy:

Grouping (Genus) Tools (Species)
Exploratory Data Analysis (EDA) Packaging of tools for quick insights; emphasis on graphics: e.g., Box-Plots, Bubble Graphs, CART, Clustering, Density Plots, Histograms, k-NN, Outlier Detection, Scatterplots, Smoothing, Time-series plots, et al.
Statistical DM (Data Mining) Rebranding of EDA; more discussion of some topics and less of others.
Statistical ML (Machine Learning) The data-analysis part of the ML packaging of statistics and data management tools with a machine learning engine, e.g., Topic Modeling, Support Vector Machines, Random Forests, Tree-Based and Rule-Based Regression and Classification, Genetic Algorithms, Gradient Boosting, Neural Networks, et al.
Statistical Learning Evolving definition, at least partly a repackaging/rebranding of Statistical ML, e.g. linear and polynomial regression, logistic regression and Discriminant Analysis; Cross-Validation/Bootstrapping, model selection and regularization methods (ridge and lasso); nonlinear models, splines and generalized additive models; tree-based methods, random forests and boosting; support-vector machines. Some unsupervised learning methods are discussed: principal components and clustering (k-means and hierarchical).
Statistical DS (Data Science) Evolving definition, rebranding of applied statistics; more discussion of some topics and less of others; this definition will continue to evolve.
Bayesian Techniques that assume a prior distribution for the parameters–it is a long story, e.g., Naive Bayes, Hierarchical Bayes, et al.
Predictive Analytics Rebranding of Predictive Modeling
Multivariate Statistics Clustering?, Factor Analysis, Principal Component Analysis, Structure Equation Modeling?, et al.
Spatial Statistics Packaging of tools for modeling spatial variability, e.g., Thin-plate splines, inverse distance weighting, geographically weighted regression.
Parametric Statistics All tools making parametric assumptions; e.g., Regression
Nonparametric Statistics All tools not making parametric assumptions; they still makes assumptions: e.g., Association Analysis, Neural Networks, Order Statistics, Rank Statistics, Quantile Regression, et al.
Semi-parametric Family of models containing both parametric and non-parametric components (e.g. Cox-proportional hazard model)
Categorical Data Analysis Tools with a categorical response, e.g., Contingency Tables, Cochran-Mantel-Haenszel Methods, General Linear Models, Loglinear Models, Logit Models, Logistic Regression, et al.
Time Series/Forecasting Tools modeling a time (or location) dependent response; e.g., ARIMA, Box-Jenkins, Correlograms, Spectral Decomposition [Census Bureau]
Survival Analysis Tools to perform time-to-event analysis (also called duration analysis) e.g., Cox Proportional Hazard, Kaplan-Meier, Life Tables, et al.
Game Theory Tools for modeling contests.
Text Analytics Tools for extracting information from text.
Cross Validation/Data Splitting e.g., K-fold Cross-Validation, Sequential Validation
Resampling Techniques With Replacement e.g., Permutation Tests, Jackknife, Bootstrapping, et al.
Six Sigma Repacking of statistics common to manufacturing with clever organizational ideas.
Quality/Process Control X-Bar Charts, R Charts, [Manufacturing]
DoS (Design of Samples) Simple Random, Systematic, Stratification, Clustering, Probabilities Proportional to Size, Multi-stage Designs, Small Area Estimation, Discrete Choice, Conjoint Analytics [Census Bureau; Marketing]
DoE (Design of Experiments) Completely Randomize, Randomized Blocks, Factorial Designs, Repeated Measures, Split-Plot, Response Surface Models, Crossover Designs, Nested Designs, Clinical Modifications [Agriculture; Pharmaceuticals]
DSim (Design of Simulation) Artificial generation of random processes to model uncertainty; Monte Carlo, Markov Chains,
Stochastic Processes Models for processes (with uncertainty), e.g., Birth-Death Processes, Markov Chains, Markov Processes, Poison Processes, Renewal Processes, et al.
Areas awaiting a name E.g., high dimensional problems (p»n); et al.

Applications of Applied Statistics

Business and Economics

Healthcare

Engineering

Social Sciences

Environmental Science

Sports Analytics

Marketing

Telecommunications

Agriculture

Education

Videos: Statistics Fundamentals

Statistics Fundamentals: These videos give you a general overview of statistics and a solid reference for statistical concepts.

Conclusion

Applied statistics is a crucial tool in various fields, providing the methods and techniques necessary to make sense of data and derive actionable insights. Understanding its key features and applications allows professionals to make data-driven decisions and solve complex problems effectively. By leveraging the power of statistical analysis, organizations and individuals can optimize operations, improve quality, and drive innovation across diverse domains.

Related Content

References

  1. Montgomery, D. C., & Runger, G. C. (2014). Applied Statistics and Probability for Engineers. Wiley.
  2. Agresti, A., & Finlay, B. (2018). Statistical Methods for the Social Sciences. Pearson.
  3. Chatfield, C. (2003). The Analysis of Time Series: An Introduction. Chapman and Hall/CRC.
  4. Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE Publications.
  5. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: With Applications in R. Springer.
  6. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer.
  7. Box, G. E. P., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time Series Analysis: Forecasting and Control. Wiley.
  8. Moore, D. S., McCabe, G. P., & Craig, B. A. (2016). Introduction to the Practice of Statistics. W. H. Freeman.
  9. Everitt, B. S., & Hothorn, T. (2011). An Introduction to Applied Multivariate Analysis with R. Springer.
  10. Kirk, R. E. (2013). Experimental Design: Procedures for the Behavioral Sciences. SAGE Publications.
  11. Applied Statistics Is A Way Of Thinking, Not Just A Toolbox
  12. Bartlett, R. (2013). A Practitioner’s Guide To Business Analytics. McGraw-Hill
  13. Afshine Amidi

Fear less, hope more, eat less, chew more, whine less, breathe more, talk less, say more, hate less, love more, and good things will be yours.

-Swedish Proverb

Published: 2020-01-10; Updated: 2024-05-01

TOP